模型占用的存储空间、模型运行时消耗的内存空间、模型运行的速度

1. CNN不同层的计算量

了解模型计算量的一种简单方法就是计算这个模型总共做了多少次浮点运算。除了计算量，内存带宽也是影响计算效率的重要因素。

1.1 乘积相加

神经网络中的绝大多数操作都是浮点数的乘法进行求和。例如：

y = w[0]*x[0] + w[1]*x[1] + w[2]*x[2] + ... + w[n-1]*x[n-1]

上式中，输入 w 和 x 是两个向量，输出 y 是一个标量 ( 实数 )。在神经网络的卷积层和全连接层中， w 是层学习到的参数，x 就是层的输入，而 y 则是层的输出的一部分，因为典型的层结构有多个输出。其中 w[0]*x[0] + ... 称为一次乘积相加操作(multiply-accumulate operations), 因此两个 n 维向量的点积含有 n 个 MACCs(乘积相加) 计算单元。

Technically speaking there are only n - 1 additions in the above formula, one less than the number of multiplications. Think of the number of MACCs as being an approximation, just like Big-O notation is an approximation of the complexity of an algorithm.

从每秒浮点运算 ( floating point operations per second, FLOPS ) 的角度来看，一次点积操作包含 2n-1 个 FLOPS，因为其中含有 n 次乘法运算和 n-1 次加法运算。

1.2 全连接层

在全连接层，所有的输入单元和输出单元相互连接。对于含有 I 个输入值和 J 个输出值的的层，权重 W 存储在 I×J 的矩阵中，因此全连接层的计算可以写作：

y = matmul(x, W) + b

矩阵乘法是有一系列点乘组合而成的。每一个点乘由输入 x 和矩阵W 的每一列运算得到。因此运算 matmul(x, W) 包含 I×J 个 MACCs 单元，和权重矩阵的元素个数相同。例如卷积层的最后输出为 (512, 7, 7), 那么经过 faltten 操作后，输入 I=512x7x7。

1.3 激活函数

通常层的后面会跟随非线性激活函数，例如 ReLU 或者 sigmoid 函数。由于激活函数没有乘法运算，因此使用 FLOPS 来衡量计算时间。
不同激活函数的计算量是不同的。ReLU 激活函数的表达式为：

y = max(x, 0)

在 GPU 上只有一次操作。假设全连接层有 J 个输出单元，ReLU函数进行了 J 次最大值操作，因此含有 J 个 FLOPS 单元。
Sigmoid 激活函数表达式为：

y = 1 / (1 + exp(-x))

由于 Sigmoid 函数包含幂运算，因此计算量比较复杂。通常将加法运算、减法运算、乘法运算、除法运算、幂运算和平方根运算称为一次 FLOPS。Sigmoid 函数中包含四种不同的运算操作，因此含有 4 次 FLOPS。假设全连接层有 J 个输出单元，那么Sigmoid 函数含有 4xJ 个 FLOPS 单元。通常激活函数只占模型总运算量的很小一部分。

1.3 卷积层

卷积层的输入和输出不是向量，而是三维 ( Height*Width*Channels ) 的特征图。假定正方形的卷积核边长为 k，那么卷积层不考虑偏置和激活函数的 MACCs 为：

k × k × Channels_in × Height_out × Width_out × Channels_out

这里使用输出的 Height 和 Width 是因为考虑到卷积时的stride, dilation factors, padding, etc。
对于卷积核为为 (3, 3, 128) 且输入为 (112, 112, 64) 的卷积计算，它的 MACCs 为：

3 × 3 × 64 × 112 × 112 × 128 = 924844032

In this example, we used “same” padding and stride = 1, so that the output feature map has the same size as the input feature map. It’s also common to see convolutional layers use stride = 2, which would have chopped the output feature map size in half, and we would’ve used 56 × 56 instead of 112 × 112 in the above calculation.

1.4 深度可分离卷积

深度可分离卷积 ( depthwise-separable convolution ) 首先在 Xception 中被使用，它将常规的卷积操作分解为 depthwise 卷积与 pointwise 卷积两个部分。该结构和常规提取特征的卷积操作类似，但是参数量和运算成本较低，在轻量级网络 ( MobileNet )中十分常见。

假设输入层为 (112, 112, 64)，经过 (3, 3, 128)的卷积核，假定使用 same padding 并且 stride=1，使得输入输出特征图大小相同，那么最终得到 (112, 112, 128) 的特征图。常规卷积示意图如下所示。 MACCs 次数为：

3 × 3 × 64 × 112 × 112 × 128 = 924844032

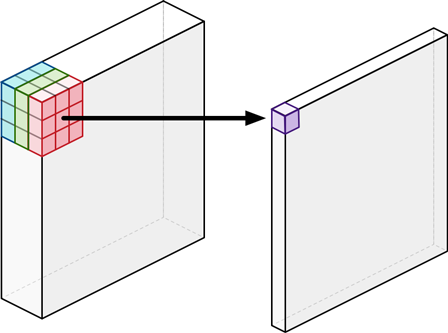
Depthwise Convolution 的每个卷积核只与输入的一个通道进行卷积，卷积核的数量与上一层的通道数相同。因此输入图像经过 depthwise 卷积之后生成 3 个单通道的特征图，如下图所示。

MACCs = K × K × Channels_in × Height_out × Width_out
      = 3 × 3 × 64 × 112 × 112 
      = 7225344

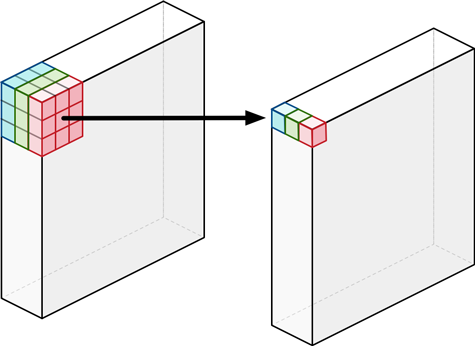
Depthwise Convolution 完成后的特征图数量与输入层的通道数相同，无法扩展特征图的数量，而且无法有效利用不同通道在相同空间位置上的特征信息。因此在 depthwise 卷积之后需要 pointwise Convolution 将特征图进行组合生成新的特征图。Pointwise Convolution 的卷积核大小为 1x1。

MACCs = 1 × 1 × Channels_in × Height_out × Width_out x Channels_out
      = 1 × 1 × 64 × 112 × 112 x 128 
      = 102760448

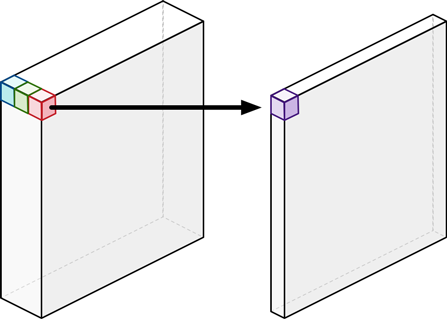
因此 depthwise-separable convolution 的 MACCs 为：

MACCs = (K × K × Channels_in × Height_out × Width_out) + (Channels_in × Height_out × Width_out × Channels_out) 
      = Channels_in × Height_out × Width_out × (K × K + Channel_out)

The exact factor is K × K × Cout / (K × K + Cout) . It should be pointed out that depthwise convolutions sometimes have a stride > 1, which reduces the dimensions of their output feature map. But a pointwise layer usually has stride = 1, and so its output feature map will always have the same dimensions as the depthwise layer’s.

1.5 批量归一化层

批量归一化层 ( Batch normalization Layer) 每一个输出的函数表达式可以写为：

z = gamma * (y - mean) / sqrt(variance + epsilon) + beta

其中 y 是上一层输出特征图的一个元素，mean 为均值，variance 为方差，epsilon 确保分母不为0，gamma为尺度因子，beta 为偏置。每一个通道都有其对应的值，因此对于通道为 c 的卷积输出层，batch normalization layer 学习的参数量为 4c。

z = gamma * ((x[0]*w[0] + x[1]*w[1] + ... + x[n-1]*w[n-1] + b) - mean) / sqrt(variance + epsilon) + beta

由于在预测过程中移除了 batch normlization layer，因此考虑模型的计算量时可以不用关注正则化层的影响。

This trick only works when the order of the layers is: convolution, batch norm, ReLU — but not when it is: convolution, ReLU, batch norm. The ReLU is a non-linear operation, which messes up the math.

1.6 池化层

对于 112, 112, 128) 的特征图，如果最大池化的 pooling size = 2 并且 stride = 2，那么 FLOPS 操作数为 112 × 112 × 128 = 1605632。可以看到，池化层的操作数远远少于卷积层的操作数，因此池化层也是网络计算复杂度的舍入误差。

2. 模型耗费的内存

在模型的每一层计算中，硬件设备需要从主存储中读取输入向量或者特征图的值，从主存储中读取权重参数并与输入计算点积，将得到的新向量或者特征图作为结果写入主存储中。这些操作都涉及到大量的内存读写，耗费的时间可能远远大于计算的次数。

2.1 权重的内存

层将权重保存在主存储中，这意味着权重参数越少，模型运行速度越快。如前文所述，输入为 I 个神经元和输出为 J 个神经元之间的权重参数为 I x J，加上偏置向量，总的参数为 ( I + 1) x J。对于大小为 k，输入通道数为 Channels_in，输出通道数为 Channels_out 的卷积层的参数为 k x k Channels_in x Channels_out 加上偏置向量参数 Channels_out。
对于输入 4096 输出为 4096的全连接层，其权重参数量为 (4096 + 1) x 4096 = 16781312。对于输入为 (64, 64, 32) 卷积核为 (3, 3, 48) 的卷积层，其权重参数量为 (3 x 3 x 32 x 48 + 48 = 13872)。可以看到，相比于卷积层，全连接层的参数量相对更多。

Fully-connected and convolutional layers are actually very similar. A convolutional layer is basically a fully-connected layer with the vast majority of the connections set to 0 — each output is only connected to K × K inputs rather than all of them, and all the outputs use the same values for these connections. This is why convolutional layers are so much more efficient about memory, since they don’t store the weights for connections that are not used.